Dev

Nov 18, 2022

Proving languages are not regular with the pumping lemma

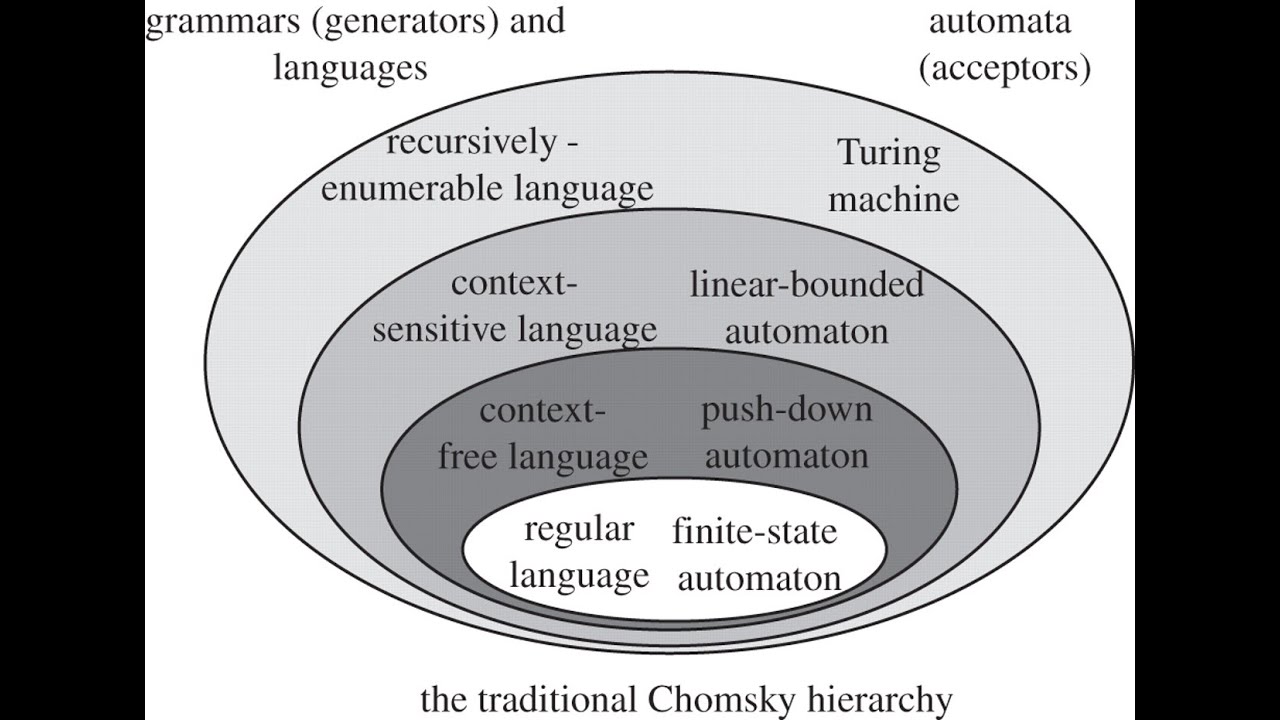
Proving that a language is regular is pretty straightforward- if a deterministic finite automaton (DFA), nondeterministic finite automaton (NFA), regular expression or a regular grammar can be constructed to represent the language then it is regular. However, claiming that a language is not regular is not as simple. There are definitely multiple ways to go about this but in this article we will explore the use of the pumping lemma. ⁠

Informal Explanation

The pumping lemma portrays a required property of regular languages. This property essentially says that all strings greater than a minimum length in a regular language can be "pumped"-- repeat a certain section of the string an arbitrary amount of times-- and result in a new string that is also in the language. This minimum length is typically referred to as p. We want to use a string w that has at least length p and split it into 3 substrings called x, y and z. The constraints of these substrings are that the length of xy is at most p, x and z can be 0 but y must be atleast 1 (y is the substring that will actually be pumped).

Formal Definition

⁠For a regular language L, there is a p >= 1 where every string w of length atleast p in L can be divided into 3 substrings that satisfy the following:

length of y is at least 1

length of xy is at most p

for all n greater than or equal to 0, xyⁿz is in L

Examples

Q: ⁠Prove that the language L = {0ⁿ1ⁿ, n >= 0} is nonregular

Proof by contradiction via pumping lemma:

Assume L is regular so the pumping lemma applies

Let p be the pumping length

Consider the string w = 0ᵖ1ᵖ, which is in the language

Express 0ᵖ1ᵖ as xyz, where length of y is at least 1 and length of xy is at most p

Since length of xy is less than p, it follows that y must be a string in the first half of w

The first half of w only consists of 0's, so y can only consist of 0's. In any case, y consists of at least one 0. For this reason, pumping will easily result in strings that are not in the language (0ⁿ1ⁿ)

Only the string xyz is in the language-- xz, xyyz, xyyyz, etc. are not in the language

This violates a condition of the pumping lemma and we have a contradiction ⁠Therefore, L is not regular!

Visualization:

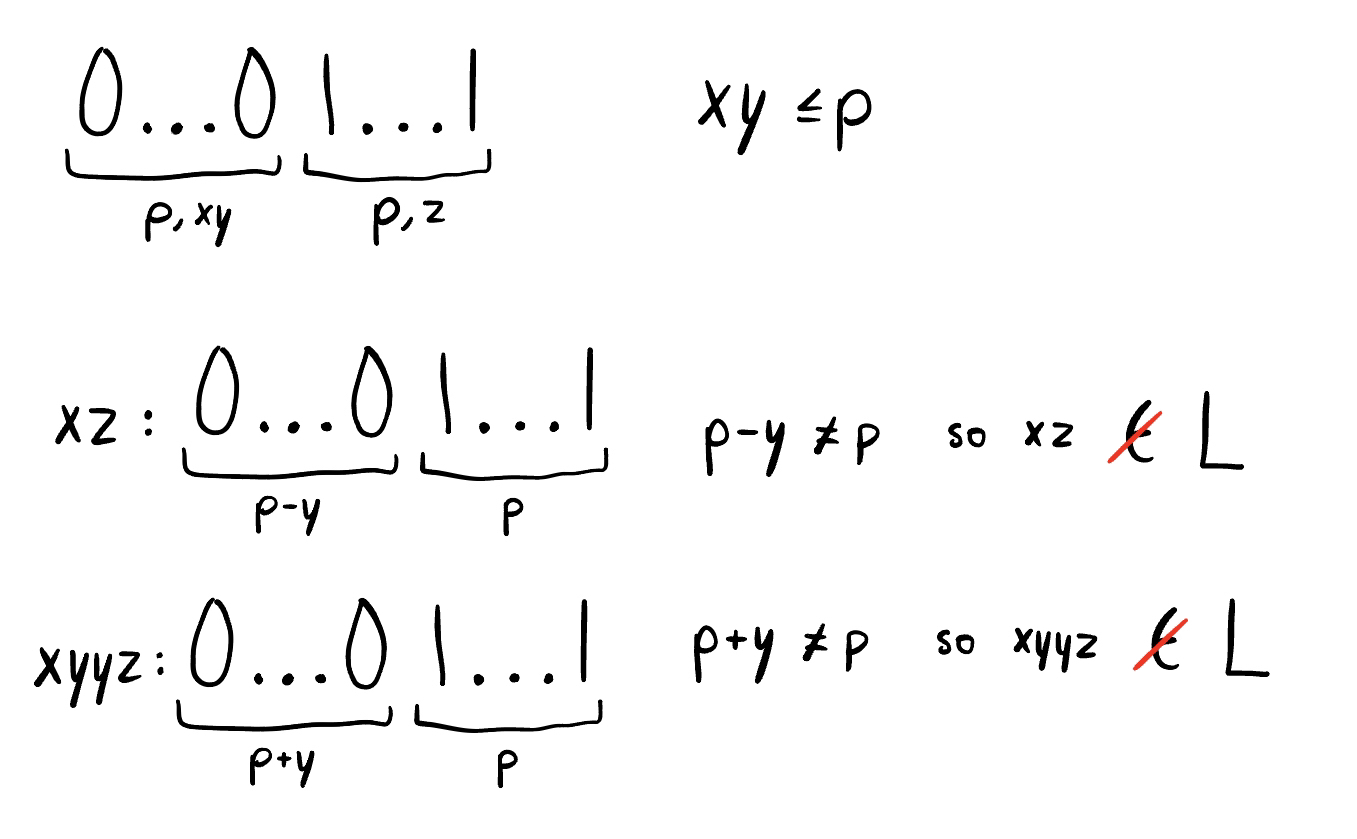
*remember y contains at least one character

⁠Common Pitfalls ⁠It is important to understand the application of the pumping lemma and the specifications to actually using it. The pumping lemma works to prove a language is not regular by considering one string in the language, all different possible values of xy, and one instance of xyⁿz. So to actually prove a language is not regular, construct one string in the language and prove that one instance of xyⁿz is not in the language for all different possible values of xy.